橘子树下

学习园地

0%

发表于 更新于 分类于 Valine：

目的

在量化分析中，经常会需要获取 \(\beta\) (贝塔收益或贝塔系数），那该如何查询或计算该系数呢？

贝塔(β)的含义

贝塔系数衡量了个股或基金相对于整个股市的波动情况。

β范围 含义
β=1 股票或基金的风险收益率与市场平均风险收益率相同
β>1 股票或基金的风险相较于市场平均更大
β<1 股票或基金的风险相较于市场平均更小
阅读全文 »

发表于 更新于 分类于 ， Valine：

目的

方差在统计描述和概率分布中各有不同的定义，并有不同的公式。
在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。
总体方差计算公式： \({\sigma}^2=\frac{\sum_{i=1}^{N}(X_i-\bar{\mu})}{N}\)
其中\({\sigma}^2\)为总体方差，\(X_i\)为变量，\(\bar{\mu}\)为总体均值，\(N\)为总体例数。

实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，
样本方差计算公式： \({S}^2=\frac{\sum_{i=1}^{N}(X_i-\bar{X})}{n-1}\)
其中\({S}^2\)为样本方差，\(X_i\)为变量，\(\bar{X}\)为样本均值，\(n\)为样本例数。

阅读全文 »

发表于 更新于 分类于 ， Valine：

目的

什么是协方差

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。 协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
\(Cov(X,Y) = E[(X-E(X))(Y-E(Y))]\)

阅读全文 »

发表于 更新于 分类于 ， Valine：

需求

在jupyter中可以直接使用用dataframe的名字输出美观的表格形式，例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import QUANTAXIS as QA

"""
通过本地数据库获取股票日线数据：
QA.QA_fetch_stock_day_adv(
    code,
    start='all',
    end=None,
    if_drop_index=True,
    collections=Collection(Database(MongoClient(host=['localhost:27017'], document_class=dict, tz_aware=False, connect=True), 'quantaxis'), 'stock_day'),
)
"""

data=QA.QA_fetch_stock_day_adv(["002003",'300999','603899'],'2021-05-12','2021-05-13')
df = data.data
df
阅读全文 »

发表于 更新于 分类于 Valine：

说明

在升级jupyter到版本6.x以上时，在启动的时候会报很多行以下错误 

1
Config option `template_path` not recognized by `LenvsLatexExporter`. Did you mean one of: `template_file, template_name, template_paths`?

解决方案

使用VS Code依次打开python安装目录下的/lib/site-packages/ ('jupyter_contrib_nbextensions', 'jupyter_latex_envs' 及'latex_envs')子目录。

通过'Edit/Replace in Files'来查找'template_path'并替换为'template_paths'。

注意有的内容已经是template_paths，不需要修改。

参考

1/ [jupyter代码自动补全插件、安装后出现警告“Config option template_path not recognized by LenvsLatexExporter”的解决方案](jupyter代码自动补全插件、安装后出现警告"Config option not recognized by "的解决方案_Sun's Blog-CSDN博客)

2/ Config option template_path not recognized by LenvsLatexExporter. Did you mean one of: template_file, template_name, template_paths? · Issue #1529 · ipython-contrib/jupyter_contrib_nbextensions (github.com))

发表于 更新于 分类于 ， Valine：

Typrora中使用了Mermaid来提供强劲的绘制流程图、时序图的功能。

关于Mermaid

是一种简单的类似 Markdown 的脚本语言，通过 JavaScript 编程语言，将文本转换为图片。因此，真正实现画图功能的并不是 Typora 本身，它只是内置了对 Mermaid 的支持。

图形介绍

流程图(flowchart)

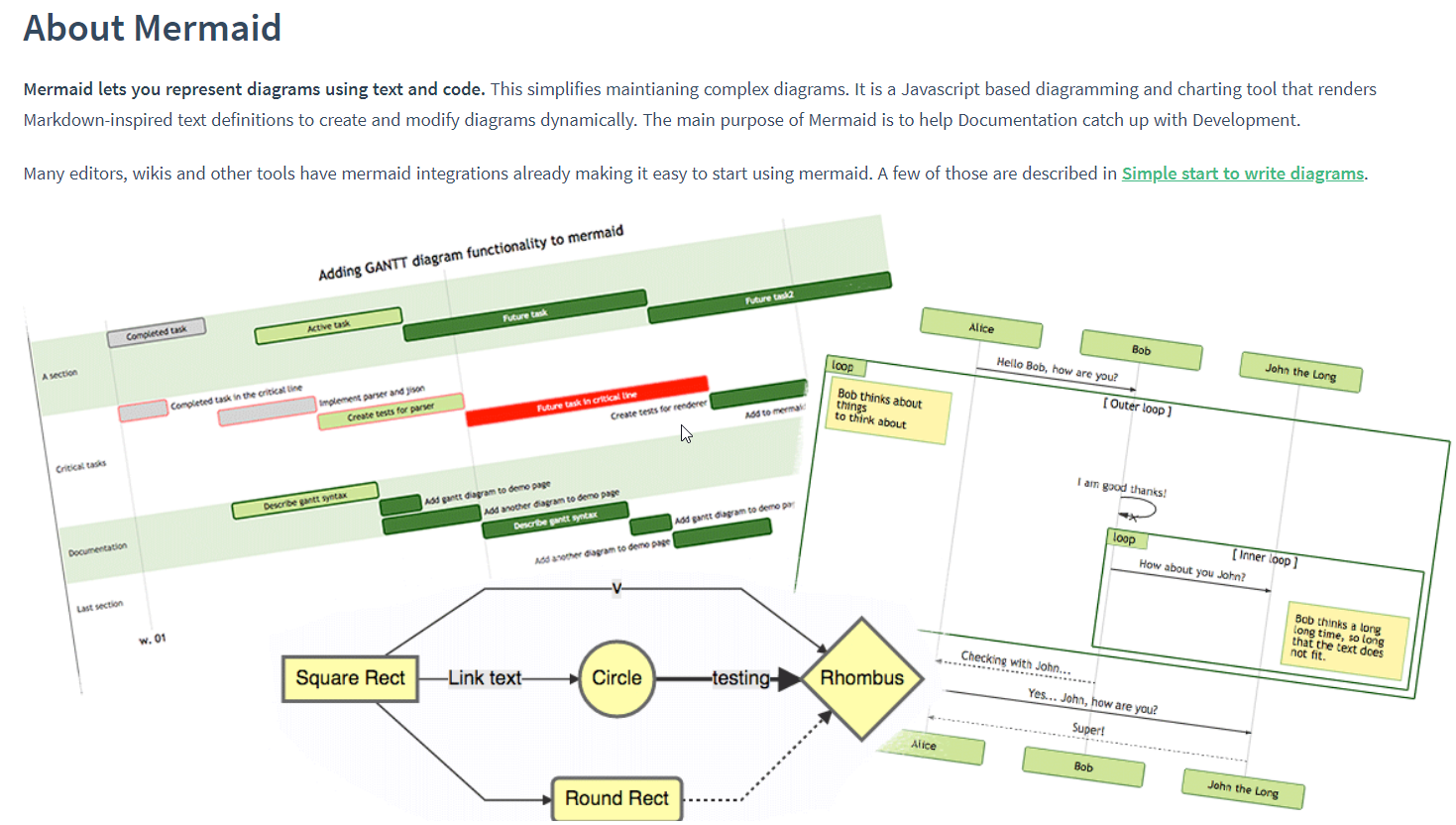
主要语法说明：

graph - 表明是流程图

方向：

  • TB - top to bottom
  • TD - top-down/ same as top to bottom
  • BT - bottom to top
  • RL - right to left
  • LR - left to right
1
2
3
4
graph TD;
    A-->B;
    A-->C;
    B-->D;
1
2
3
4
graph TD;
    A-->B;
    A-->C;
    B-->D;

时序图

语法解释：->> 代表实线箭头，-->> 则代表虚线。

参考

[1] Mermaid:https://mermaid-js.github.io/mermaid/#/

发表于 更新于 分类于 ， Valine：

可以利用队列或管道来进行多进程下的日志输出，但官方文档推荐了一种利用logging.SocketHandler的方案来实现多进程日志输出。

其原理是：多个进程将各自环境下的日志通过Socket发送给一个专门打印日志的进程，这样就可以防止多进程打印的冲突与混乱情况。