基本概念

标量、向量、矩阵和张量

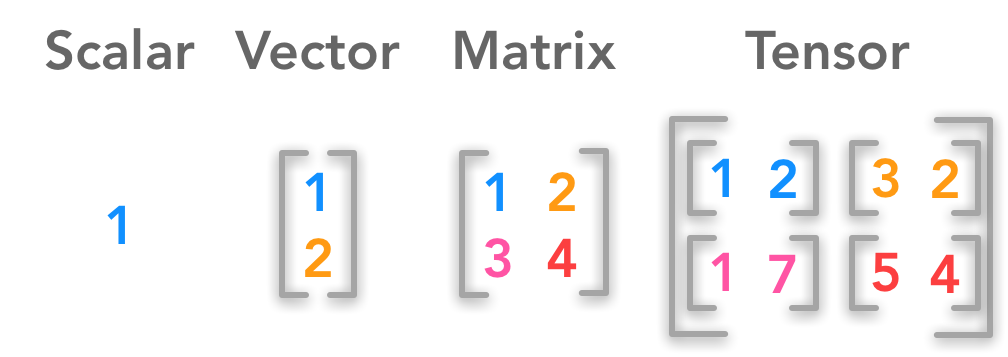
• 标量（scalar）：一个标量就是一个单独的数，它不同于线性代数中研究的其他大部分对象（通常是多个数的数组）。
• 向量（vector）：一个向量是一列数。这些数是有序排列的。
• 矩阵（matrix）：矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个）所确定。
• 张量（tensor）：在某些情况下，我们会讨论坐标超过两维的数组。一般地，一个数组中的元素分布在若干维坐标的规则网格中，我们称之为张量。

转置

转置（transpose）是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像，这条从左上角到右下角的对角线被称为主对角线（main diagonal）。

向量可以看作只有一列的矩阵。对应地，向量的转置可以看作是只有一行的矩阵。

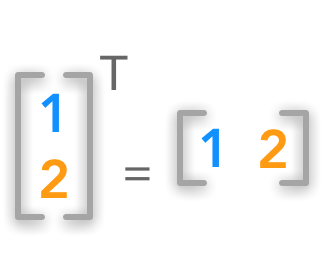
方阵的转置

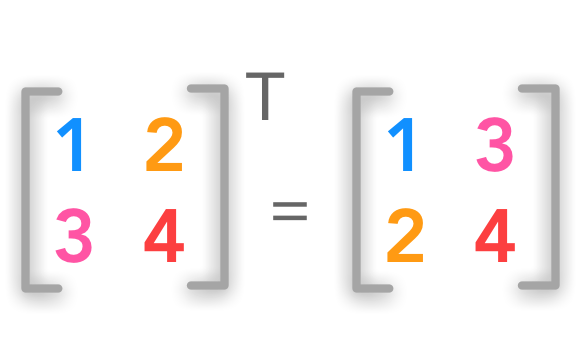
非方阵的转置

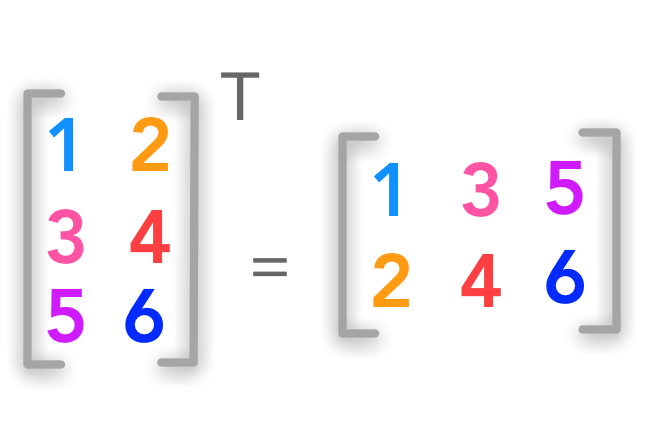
上标 \(^\text{T}\)用来表述转置矩阵

\({A}= \begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \\ A_{3,1} & A_{3,2} \end{bmatrix}\) 的转置矩阵为：

\({A}^{\text{T}}= \begin{bmatrix} A_{1,1} & A_{2,1} & A_{3,1} \\ A_{1,2} & A_{2,2} & A_{3,2} \end{bmatrix}\)

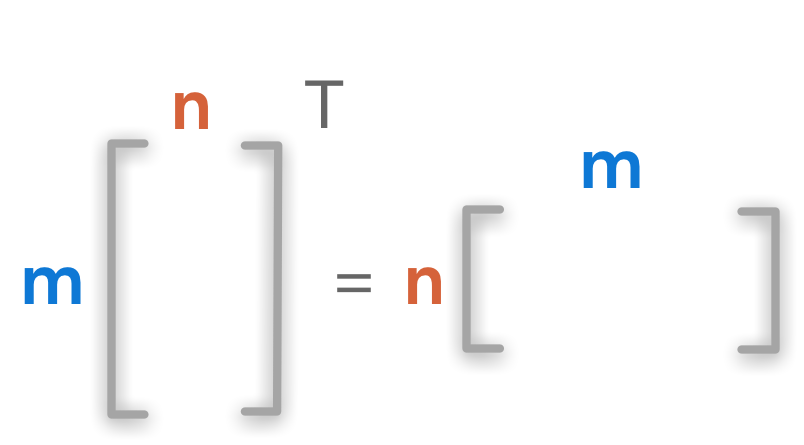
矩阵的形状 (\(m \times n\)) 在转置后变为 (\(n \times m\)).

线性方程组

对于一个线性方程组

\(\large \begin{equation} \left\{ \begin{aligned} x_1+x_2=2\\ x_1-x_2=4\\ \end{aligned} \right. \end{equation}\)

这里有两个方程和两个变量，一般可以得到唯一解或无穷多解。利用线性代数可以对其进行简洁地表示和运算。线性代数的运算离不开矩阵，矩阵是按照长方阵列排列的实数或复数集合。例如存在矩阵

\(\large A=\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right], X=\left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right], b=\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]\)

这样，上述线性方程组可记为\(AX=b\).

即： \(\large \left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right]=\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]\)

假想
\(\large \frac{1}{\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right]}\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right]=\frac{1}{\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right]}\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]\)

得： \(\large \left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right]=\frac{1}{\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right]}\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]\)

示例

在Python中，使用numpy库可以方便的进行矩阵操作。

使用numpy来创建向量(vector)

\({x} =\begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_n \end{bmatrix}\)

创建指定长度及数值的向量

1
2
3

import numpy as np
x = np.array([1,2,3,4])
x

array([1, 2, 3, 4])

创建指定长度及随机数值的向量

1 2	x = np.random.randint(1,10,size=10) x

array([8, 2, 2, 6, 5, 7, 5, 4, 4, 4])

使用numpy来创建矩阵(matrix)

\({A}= \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \cdots & \cdots & \cdots & \cdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix}\)

创建指定长度及数值的矩阵

例如：\(3 \times 2\) 的矩阵

1 2	A = np.array([[1, 2], [3, 4], [5, 6]]) A

array([[1, 2],
       [3, 4],
       [5, 6]])

创建指定长度及随机数值的矩阵

例如：\(3 \times 2\) 的矩阵

1 2	A = np.random.randint(1,10,size=(3,2)) A

array([[6, 5],
       [7, 5],
       [7, 6]])

利用numpy来进行矩阵转置

1 2	A = np.array([[1, 2], [3, 4], [5, 6]]) A

array([[1, 2],
       [3, 4],
       [5, 6]])

1 2	A_t = A.T A_t

array([[1, 3, 5],
       [2, 4, 6]])

1 2	print(A.shape) print(A_t.shape)

(3, 2)
(2, 3)

求解线性方程组

求二元一次线性方程组

\(\large \begin{equation} \left\{ \begin{aligned} x_1+x_2=2\\ x_1-x_2=4\\ \end{aligned} \right. \end{equation}\)

的解。

分析：如章节1.3中所述。
\(\large A=\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right], X=\left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right], b=\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right].\)

这样，上述线性方程组可记为\(AX=b\).
则：\(X=\large\frac{1}{A}b\)

即：\(\large \left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right]=\frac{1}{\left[ \begin{matrix} 1 & 1 \\ 1 & -1 \\ \end{matrix} \right]}\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]\)

说明：
\({A}\)的逆矩阵表述为\({A}^{-1}\). 逆矩阵满足如一条件。

\({A}^{-1}{A}={I}_n\)

NumPy 提供了线性代数函数库 linalg，该库包含了线性代数所需的所有功能，可以看看下面的说明：

函数	描述
`dot`	两个数组的点积，即元素对应相乘。
`vdot`	两个向量的点积
`inner`	两个数组的内积
`matmul`	两个数组的矩阵积
`determinant`	数组的行列式
`solve`	求解线性矩阵方程
`inv`	计算矩阵的乘法逆矩阵

计算过程如下：

import numpy as np

#创建矩阵A, 这里用了两种方法，实际中A1 =A2
A1 = np.mat('1 1;1 -1')
A2 = np.array([[1, 1], [1,-1]])
b = np.array([2,4])

#用solve函数求解线性方程
X1 = np.linalg.solve(A1,b)
X2 = np.linalg.solve(A2,b)
print(X1)
print(X2)

[ 3. -1.]
[ 3. -1.]

此外，也可利用先求A的逆矩阵，然后和b进行点积求解。

A = np.array([[1, 1], [1,-1]])
b = np.array([2,4])

#使用点积的两种方式
X1 = (np.linalg.inv(A)).dot(b)
X2 = np.dot(np.linalg.inv(A),b)
print(X1)
print(X2)

[ 3. -1.]
[ 3. -1.]

线性回归模型简介

假设被解释变量\(y\)与多个解释变量\(X_1,X_2,...,X_p\)之间具有线性关系，则记为

\(\large y=\beta_0+\beta_1X_1+\beta_2X_2+...+\beta_pX_p+\mu\)

称之为多元线性回归模型，其中\(\beta_0,\beta_1,...,\beta_p\)为\(p+1\)个未知参数，\(\mu\)为随机扰动项，表示除\(X_1,X_2,...,X_p\)以外影响\(y\)的所有非观测因素，并假设\(\mu\sim N(0,\sigma^2)\)。

假设有\(n\)组观测数据\(y_i,X_{1i},X_{2i},...,X_{pi},i=1,2,...,n\)，则存在线性方程组

\(\large \begin{equation} \left\{ \begin{aligned} y_1=\beta_0+\beta_1X_{11}+\beta_2X_{21}+...+\beta_pX_{p1}+\mu_1\\ y_2=\beta_0+\beta_1X_{12}+\beta_2X_{22}+...+\beta_pX_{p2}+\mu_2\\ \vdots\\ y_n=\beta_0+\beta_1X_{1n}+\beta_2X_{2n}+...+\beta_pX_{pn}+\mu_n\\ \end{aligned} \right. \end{equation}\)

若记

\(Y=(y_1,y_2,...,y_n)^\tau， X=\left[ \begin{matrix} 1&X_{11} & X_{21}&...&X_{p1} \\ 1&X_{12} & X_{22}&...&X_{p2} \\ \vdots & \vdots&\ddots\\ 1&X_{1n} & X_{2n}&...&X_{pn} \\ \end{matrix} \right]，\beta=(\beta_1,\beta_2,...,\beta_n)^\tau，\mu=(\mu_1,\mu_2,...,\mu_n)^\tau\) 则线性方程组可表示为

\(\large Y=X\beta+\mu\)

通过参数估计方法，可以得到未知参数\(\beta\)的估计值。参见计量经济学：多元线性回归的最小二乘估计

\(\large \hat{\beta}=(X^\tau X)^{-1}X^\tau Y\)

线性回归模型求解模拟

statsmodels是Python中一个强大的统计分析包，包含了回归分析、时间序列分析、假设检验等等的功能，当需要在Python中进行回归分析时，就可以导入statsmodels。

statsmodels.regression.linear_model里有回归函数statsmodels.OLS，它的输入参数有(endog, exog, missing, hasconst)。一般只考虑前两个输入，其中，endog是回归中的因变量\(Y\)，是一个\(n\)维的向量；exog是回归中的自变量\(X_1,X_2,...,X_P\)，由于statsmodels.OLS不会假设回归模型有常数项，所以我们应该假设模型是

\(\large y_t=\beta_0X_{0t}+\beta_1X_{1t}+\beta_2X_{2t}+...+\beta_pX_{pt}+\mu,t=1,2,...,n\)

其中，对所有\(t=1,2,...,n\)，令\(X_{0t}=1\)。因此，exog的输入是一个\(n\times (p+1)\)的向量。

statsmodels.OLS的输出结果是statsmodels.regression.linear_model.OLS类，并没有进行任何运算。在OLS的模型之上调用拟合函数 fit()，才进行回归运算，并且得到statsmodels.regression.linear_model.RegressionResultsWrapper，它包含了这组数据进行回归拟合的结果摘要。调用params可以查看计算出的回归系数\(\beta_0,\beta_1,...,\beta_p\)。下面将分连续变量和离散变量两种情况来模拟求解线性回归模型。

橘子树下

线性代数在量化投资分析中的应用